| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- nosql
- spring
- BFS
- java
- 자료구조
- OS
- 운영체제
- 플로이드-워셜 알고리즘
- Data structure
- javascript
- 데이터베이스
- DFS
- Algorithm
- 영속성 컨텍스트
- HTML
- jpa
- 프로그래머스
- 알고리즘
- It
- Docker
- db
- mysql
- 완전탐색
- CS
- 트랜잭션
- CSS
- websocket
- 백준
- redis
- PYTHON
Archives
- Today
- Total
If at first you don't succeed, try again
[자료구조] Priority Queue(우선순위 큐)(Python) 본문
* 개요
Priority Queue(우선순위 큐)는 선입선출 구조를 가지는 일반적인 큐의 자료구조와는 달리, 데이터의 삽입은 순서와 관계가 없지만 삭제할 때는 우선순위가 높은 원소부터 삭제가 되는 자료구조이다. 우선순위 큐의 대표적인 예로 heap이 있다.
* Heap(힙)
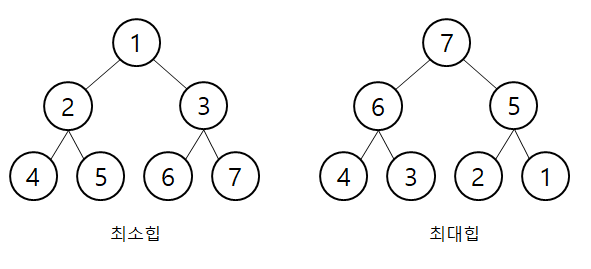
heap(힙)은 여러 개의 값 중에서 가장 크거나 가장 작은 값을 빠르게 찾기 위해 만든 이진 트리이다. 힙의 종류에는 최대 힙과 최소 힙이 있는데, 최대 힙은 root 노드에 가장 큰 값이 들어가게 되며, 최소 힙은 root 노드에 가장 작은 값이 들어가게 된다. 힙의 데이터 삽입 및 삭제의 시간 복잡도는 O(logN)이 소요된다.
* 파이썬으로 구현한 우선순위 큐(최소 힙)
우선순위 큐를 위해서 파이썬에 내장되어 있는 heapq 모듈을 import 하였다.
import heapq
heap = []
heapq.heappush(heap, 1)
heapq.heappush(heap, 5)
heapq.heappush(heap, 4)
heapq.heappush(heap, 2)
heapq.heappush(heap, 3)
print(heap) # 1 2 4 5 3
# 최소 힙
while heap:
print(heapq.heappop(heap), end = " ") # 1 2 3 4 5heapq 모듈은 pop을 할 때 최소힙을 기준으로 pop을 하므로, 원소가 작으면 작을수록 우선순위를 더 높게 둔다. 따라서 출력을 하였을 때, 1 2 3 4 5 순으로 출력이 된다.
* 파이썬으로 구현한 우선순위 큐(최대 힙)
import heapq
heap = []
max_heap = [] # 최대 힙
heapq.heappush(heap, 1)
heapq.heappush(heap, 5)
heapq.heappush(heap, 4)
heapq.heappush(heap, 2)
heapq.heappush(heap, 3)
for i in heap:
heapq.heappush(max_heap, (-i, i))
print(max_heap)
while max_heap:
print(heapq.heappop(max_heap)[1], end = " ") # 5 4 3 2 1heapq 모듈은 최소힙을 기준으로 하고 있다. 이를 최대 힙으로 만들기 위해서는 반복문을 통해 기존 요소에 -1을 곱하여 우선 순위를 역순으로 하여 max_heap에 push해주면 된다.
'Computer Science > 자료구조(Python)' 카테고리의 다른 글
| [자료구조] Deque(덱)(Python) (0) | 2022.11.07 |
|---|---|
| [자료구조] Circular Queue(원형 큐)(Python) (0) | 2022.11.07 |
| [자료구조] Queue(큐)(Python) (0) | 2022.11.04 |
| [자료구조] Stack(스택)(Python) (0) | 2022.11.02 |
| [자료구조] Circular LinkedList(원형 연결리스트)(Python) (0) | 2022.11.01 |




